

آنچه در این مقاله میخوانید [پنهانسازی]
در اینترنت ها ، لایه های شبکه ای با دریافت کردن دیتاگرام از نقطه شروع به یک یا چند مقصد استفاده می کنند . چنانچه دیتاگرام تنها برای یک مقصد ارسال شود ، الگوی دریافت یک به یک را داریم که مسیریابی تکپخشی (unicast) می نامند . چنانچه دیتاگرام ها برای چند مقصد ارسال می شود یک تحویل یکبهچند داریم که مسیریابی چندپخشی (Multicast) می نامند.
در دنیای شبکههای ارتباطی ، مسیریابی در صورتی مقدور می باشد که روتر یک نمودار می فرستد تا پک هایی را که به گره بعدی در راه منتقل می کند تا در نهایت به مقصد مورد نظر برسد . برای ساختن جداول فوروارد روتر ، اینترنت از پروتکلهای مسیریابی متفاوتی استفاده می نماید که وضعیت های پویایی دارد . نمودار های مسیریابی روترها بهطور پیدرپی آپدیت میشوند .
مسیریاب های یونیکست در اینترنت ، با مقدار بسیاری روتر ، میزبان و بر مبنای مسیریاب سلسلهمراتبی در چند مرحله با بهره برداری از الگوریتمهای مسیریاب اجرا می گردد. در مسیریابی یونیکست ، پک ها توسط جداول فوروارد ، از نقطه شروع کننده به مقصد و از یک هاپ به هاپ بعدی فرستاده می شوند. میزبان نقطه شروع احتیاجی به فرستادن نمودار ندارد، چون پک خود را به روتر پیشفرض در شبکه های بومی تحویل میدهد.
میزبان مقصد هم احتیاجی به فرستادن نمودار ها نخواهد داشت ، چون پک را از روتر پیشفرض در شبکه محلی دریافت می نماید . این عرض بدان مفهوم هست که فقط روترهایی که شبکهها را در اینترنت به یکدیگر وصل می نمایند به جداول فرستاده شده احتیاج دارند. با تعریف فوق بایستی بگوییم که مسیریابی یک پک از مبدأ به مقصد بهمعنی مسیریابی پک از روتر مبدأ (روتر پیشفرض میزبان مبدا) به روتر مقصد (روتر وصل شده به شبکه مقصد) هست.
گرچه یک پک بایستی از مسیریابهای مبدأ و مقصد عبور نماید، منتها پرسش این هست که پک بایستی از چه مسیریابهای دیگری گذر بکند یا به عبارت دیگر، چند راه وجود دارد که یک بسته از نقطه شروع تا مقصد را طی کند .
برای پیدا کردن بهترین راه ، اینترنت را میتوان بهشکل یک نمودار تصور کرد. برای طراحی اینترنت بهعنوان یک نمودار، میتوان روتر ها را مثل یک گره و هر شبکه را در میان چند تا روتر بهعنوان یک کناره در نظر بگیریم. اینترنت در حقیقت بهعنوان یک گراف وزندار طراحی می گردد که در آن هر حاشیه هزینه هایی دارد.
چنانچه از گراف وزندار برای نمایشدادن یک ناحیه جغرافیایی بکار بگیریم ، گرهها میتوانند ناحیه ها و لبهها میتوانند راه هایی باشند که منطقه ها را بههم وصل میکنند . وزنها در این درباره، فاصله های میان شهری می باشد . با این حال ، در مسیریابی ، هزینه یک حاشیه در پروتکلهای مسیریاب گوناگون فرق دارند . فرض بکنید هزینهای برای هر حاشیه وجود دارد . درصورتیکه اصلاً لبهای میانه گرهها وجود نداشته بود ، هزینه ها بی نهایت گران می شود .
وقتی که اینترنت را بهعنوان یک گراف وزندار طراحی می نمائیم، یکی از راههای شرح بهینه ترین مسیرها را از روتر نقطه شروع شونده به روتر مقصد با محاسبه کمترین هزینه میان دو نقطه می باشد . بهعبارت دیگر ، روتر مبدأ مسیری را برای رسیدن به روتر مقصد تعیین میکند به شکلی که هزینه های کل مسیر کمترین هزینه را میان تمامی راه های ممکن می توان داشته باشد . در تصویر ۱ ، عالی ترین راه میان A و E ، A -B -E با هزینه 6 می باشد . این بدین معنی هست که هر روتر الزاماً باید راه کمهزینه میان خود و دیگر روترها را نمایان کند تا بتواند یک پک را در کمترین تایم برای مقصد فرستاده می شود .
درصورتیکه روتر N در اینترنت موجود باشد ، (N -1) بیانکننده راه های کم هزینه از هر روتر به روتر دیگر می باشد . این بدین معنی هست، که ما به راه های کمهزینه N×(N -1) احتیاج داریم تا پهنای باند شبکه بیهوده به هدر نرود.
به طرز مثال ، درصورتیکه فقط 10 روتر در اینترنت داشتیم، به 90 راه کمهزینه احتیاج داریم . یک مسیر بهتر برای رویت کردن این راه ها ، ترکیب آنها در شکل یک درخت کمهزینه می باشد. درخت کمهزینه درختی با روتر مرجع بهعنوان ریشه هست که کل گرهها ی تحت شبکه از آن دیدار میکنند و در آن راه میان ریشه و هر گره کمترین است.
در این مورد ، یک درخت ، کمترین راه را برای هر گره دارا است . در دنیای حقیقی ، ما N درخت راه های کمهزینه برای کل اینترنت داریم ، با این وجود، بعضی از آنها اهمیت بسیاری دارد. شکل ۲ هفت درخت کمهزینه مناسبت استفاده در اینترنت را نمایش میدهد . یکی از راه های کمهزینه از X به Y در درخت X معکوس راه کمهزینه از Y به X در درخت Y می باشد.
هزینه در هر دو طرف یکی هست . برایمثال ، در شکل ۲ ، راه A به F در درخت A بهصورت (A → B → E → F) می باشد ، ولی راه ها از F به A در درخت F بهصورت (F → E → B → A) می باشد . در هر مورد مبلغ برابر با 8 می باشد، یکی از راه های کمهزینه از X به Y در درخت X معکوس راه کمهزینه از Y به X در درخت Y می باشد . هزینه در هر دو طرف یکی هست . برایمثال ، در شکل ۲ ، راه A به F در درخت A بهصورت (A → B → E → F) می باشد ، ولی راه ها از F به A در درخت F بهصورت (F → E → B → A) می باشد . در هر مورد مبلغ برابر با 8 می باشد .
بهجای حرکت دادن از X به Z با مصرف از درخت X ، میتوان از X به Y با صرف از درخت X لرزش ایجاد کنه و از Y به Z با بهره برداری از نهال Y بقیه دهیم . بهعنوان مثال ، در تصویر۲ ، میتوان از A به G در درخت A با استفاده از راه (A → B → E → F → G) حرکت کنیم . به اضافه اینکه ، میتوانیم در درخت A از A به E بریم (A → B → E) و سپس در درخت E با استفاده از راه (E → F → G) کار را دنبال نمائیم . تلفیق دو راه در حالت دوم، همان مسیر روش اول می باشد . در نتیجه هزینه در مورد آغاز 9 و در مورد دوم نیز 9 (6 + 3) می باشد .
درخت های کمهزینه و نمودار های ارسال شده یکی از مولفههای کلیدی می باشند که پروتکل شبکه برای فرستادن پک ها را با کمترین خرج از آن استفاده میکند . فرآیند های مسیریابی مولفه جدی دیگری می باشند که نقش کلیدی در این عرصه را دارد . تا به امروزه ، الگوریتمهای مسیریابی گوناگون مدلسازی شدهاند . این الگوریتمها در روش شرح کمترین هزینه و متد تولید درخت های کمهزینه برای هر گره با یکدیگر گوناگون می باشند .
مسیریاب های بردار مسافت (DV) به اسم Distance -Vector برای پیدا کردن بهترین مسیر ها استفاده می شود . در مسیریاب های بردار فاصله ، اولین مسئله ای که هر گره می سازه، درخت های کمهزینه تری با اطلاعات ابتدایی میباشد، که در مورد همسایگان نزدیک است . درختان ناتمام میان همسایگان فرستاده و دریافت میشوند تا رفتهرفته درختان به طورکامل قابل استفاده در دیتا تبدیل شوند.
میتوان گفت که در مسیریاب بردار فاصله ها، یک روتر بهطور پیاپی به کل همسایه های خود درخصوص آنچه که در مورد کلیه دیتا ها میداند اطلاعرسانی می نماید، اگرچه این اطلاع رسانی ناتمام می باشد . پیش از اینکه نشان بدیم که چطوری درختان ناتمام کم خرج را میشه ترکیب کرد تا درختهای کامل تشکیل بشه، الزاماً باید به دو بخش مهم معادله بلمن –فورد، به معنای بردار که به آن ها باید توجه کنیم .
در مسیریاب بردار فاصله ، معادله بسیار معروفی به اسم بلمن -فورد قرار دارد. این معادله برای پیدا کردن پایین ترین مبلغ (کوتاهترین فاصله) بین گره مبدا x ، گره مقصد y و از روش بعضی از گرههای میانجی گر(a , b , c , …) مورد استفاده قرار میگیرد، تا پول بین منبع و گرههای میانجی گر شمارش شود و با کم ترین هزینه بین گرههای میانجی گر و مقصد داده بهدست آید، در فرمول زیر Dxy مقدار کمی از این فاصله ها را نشان میدهد .
Dxy=min{(cxa+Day), (cxb + Dby), (cxc + Dcy), …}
در مسیریاب بردار فاصله ، الزاماً باید توجه داشته باشیم که حداقل هزینه های موجود را با میزان کم مبلغ از روش یک گره واسطه ، مشابه z ، بروز رسانی میکنیم تا مشاهده کنیم که گره دوم کوتاه است یا نه . در این حالت، معادله را میتوان بهشکل آسان تری نوشت:
Dxy=min{Dxy, (cxz+Dzy)}
معادله بلمن -فورد به ما اجازه میده که از راه های کمهزینه پیشین، یک روش کمهزینه جدید بسازیم . در شکل3 ، میشه (a → y) ، (b → y) و (c → y) بهعنوان راه کمهزینه قبلی و (x → y) ) بهعنوان یک راه کمهزینه جدید درصورتیکه در نظر داشته باشیم، و معادلههای تازه را بهعنوان پدید آورنده یک درخت کمهزینه جدید از درخت کمهزینه قدیمی استفاده می نمائیم. به بیان دیگه استفاده از این معادله ها در مسیریابهای بردار مسافت شاهد این سوال است که در این روش از درختان کمهزینه برای پیدا کردن بهترین راه مورد استفاده قرار می گیرد.

بردار فاصله ، ستون مسیریاب بردار فاصله ها را تشکیل می دهد . درخت کمهزینه ترکیب راه های کمهزینه از ریشه درخت به همه مقاصدها می باشد . این مسیرها بهصورت گرافیکی به یکدیگر وصل میشوند تا درخت ها را بسازند . مسیریاب بردار فاصله این راه ها را باز می نماید تا بتواند یک بردار مسافت و یک آرایه بعدی برای نمایشدادن درخت توصیف بکند .
اکنون میدانیم یک بردار فاصله میتواند مسیر کمهزینه را در یک درخت کمهزینه نمایش دهد ، منتها بهچه نحو هر گره در اینترنت بردار مخصوص به خود را تشکیل می دهد . هر گره در اینترنت ، موقعی که وارد قسمت عملیاتی می گردد ، یک بردار فاصله خیلی ابتدایی با دستکم اطلاعاتی که از گره همسایه خود بهدست آورده تشکیل می نماید. گره ، پیغام های خوشامدگویی را برای واسطه های همسایه می فرستد، تا ماهیت همسایگان و فاصله میان خودش و هر همسایه را پیدا کند. در دنباله، با ثبت فصل های پیدا شده در یاخته های مربوطه ، یک بردار فاصله آسان را میسازد و میزان سلول دیگه را بی نهایت در بر میگیرد .
آیا این بردار فاصله نشان دهنده مسیر کمهزینه می باشند؟ در ابتدا کار اینطور بهنظر میرسد . در ابتدای کار که تنها مسافت میان دو گره را میدانیم ، راه ابتدایی بهعنوان کمهزینهترین راه در نظر گرفته می گردد ، ولی بهتدریج که اطلاعات کامل می شود، علم دقیقتری در ارتباط با کمهزینهترین راه بهدست میآید . تصویر ۴ بردار فاصلهای را که اینترنت از آنها بکار می گیرد را نمایش میدهد . توجه داشته باشید این بردار بهصورت غیرهمزمان تهیه میشوند .
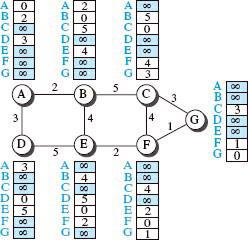
این بردارهای اولی نمیتوانند به شبکه اینترنت برای فرستادن بهینه یک جعبه یاری کنند . در تصویر ۴ ، گره A گمان می نماید که به گره G وصل نبوده ، به دلیل اینکه سلول مشخص شدهمقدار کم مخارج را خیلی زیاد نمایش می دهد . برای سلامت راندمان های این بردار ، گرهها در اینترنت حتما باید با جابه جا کردن اطلاعات به یکدیگر یاری کنند .بعد از اینکه هر گره بردار خویش را تشکیل دهد ، یه کپی از بردار برای تمام همسایه های همجوار فرستاده می شود . بعد از اینکه یک گره بردار مسافت را از همایسگان خود دریافت کرد، بردار مسافت خودش را با بکارگیری از معادله بلمن -فورد (مرحله دو) آپدیت می نماید.
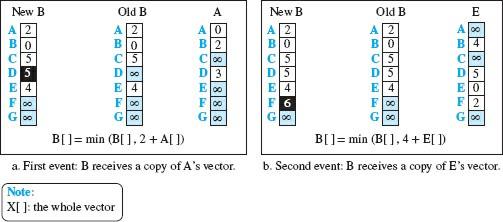
در تصویر بالا ، دو رویداد غیرهمزمان را رویت می نمائیم که یکی پس از دیگری با مسافت های زمانی اتفاق میافتد . در ماجرا یک ، گره A بردار خودش را به گره B میکند . گره B بردار خودش را با بکارگیری از مخارج cBA = 2 آپدیت می نماید . در قضیه دوم ، گره E بردار خویش را برای گره B فرستادن به جا می آورد و گره B حامل خودش را با صرف از cEA = 4 به هنگام عمل می کند.
پسازآن از نخستین ماجرا ، بردار گره B بخشی سلامت معلوم میکند و دستکم مخارج آن برای گره D بینهایت به 5 ( توسط گره A) تغییر میکند. سرانجام از ماجرا دوم، بردار گره B باز هم سلامت نمایان شده حداقل مخارج آن برای گره F از بینهایت به 6 (توسط گره E) تغییر داده می شود، تعویض بردارها در نهایت راندمان شبکه را استوار می نماید و به گرهها رخصت می گیرد حداقل مبلغ را میان خود و گره های دیگه پیدا می کند. توجه کنید که پس از آپدیت کردن یک گره ، بلافاصله بردار آپدیت شده را برای کل همسایگان فرستاده می شود . حتیدرصورتیکه همسایه ها از بردار های قدیمی استفاده می کنند ، بازهم ورژن آپدیت شده را بدست می آورد .
خط های 4 تا 11 بردار گره را میزان ابتدایی میکنند . خط های 14 تا 23 نمایش میدهد که چطور میشه بردار کنونی را پس از ارسال بردار تازه از همسایگان آپدیت نمود . حلقه for خط های 17 تا 20 اجازه میدهد همه درگاه های ورودی (سلولها) در بردار پس از ارسال بردار تازه آپدیت میگردند . دقت کنید که گره ، بردار خودشان را در خط 12 پس از مقداردهی مقدماتی در خطوط 22 پس از آپدیت فرستاده میشود.

